Trigonometria com Funções
Na Trigonometria existe três pares de nomes. O primeiro é o Seno e Cossecante, o segundo é Cosseno e Secante, já o terceiro é Tangente e Cotangente. E para cada um dos pares tem-se diferentes circunferências:
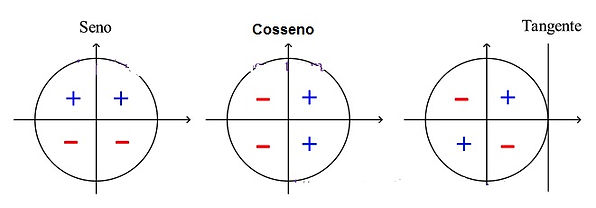
OBS: Quando se olha uma cirfunferência, sempre se olha em sentido anti-horário. E para lembrar-se da circunferência da Tangente, basta multiplicar o valor de um quadrante da circunferência do Seno pelo mesmo quadrante da circunferência do Cosseno. Exemplo: + x + = + (primeiro quadrante); + x - = - (terceiro quadrante).
Relações Fundamentais
As relações fundamentais são cinco:
sen²x + cos²x = 1
tgx = senx/ cosx
cotgx = cosx / senx
secx = 1 / cosx
cossecx + 1 / senx
Valores Notáveis
Para uma regra geral e lembrar de todos os valores dos senos, cossenos e tangentes, existe uma circunferência:
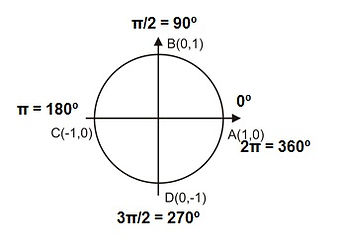
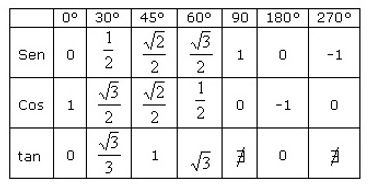
Para saber usar a circunferência, você deve saber que seno é igual à ordenada Y e o cosseno é igual a ordenada X. E saber também que se olha no parenteses que X vem primeiro e Y depois (X,Y). Então podemos dizer que o seno de 180º = 0 e o seno de 180º = -1. E um macete é dizer rápido a frase "seno e cosseno", que pensando rápido também fica SENOY COSSENO, pois o seno equivale ao Y.
Função Circular da Função Seno
Na Função Seno há uma curva chamada Senóide, o Conjunto domínio é D = IR, a Imagem é -1 ≤ senx ≤ 1, e para determinar o Período de uma função, utiliza-se p = 2π / K, onde K é o número que multiplica X. Por exemplo: 3x -> p = 2π / 3.
Exercícios:


1. Calcule os valores reais de m, fazendo que senx = 2m -1
R: senx = 2m -1
-1 ≤ senx ≤ 1
-1 ≤ 2m - 1 ≤ 1
-1 + 1 ≤ 2m ≤ 1 + 1
0 ≤ 2m ≤ 2
0/2 ≤ m ≤ 2/2
0 ≤ m ≤ 1
2. Calcules os valores reais de m, fazendo com que senx = m² + 2m + 1
R: senx = m² + 2m + 1
-1 ≤ m² + 2m + 1 ≤ 1
-1 ≤ m² + 2m + 1 m² + 2m + 1 ≤ 1
0 ≤ m² + 2m + 2 m² + 2m ≤ 0 llllllllllllllllllllllllll
Δ = 4 - 8 m(m + 2) = 0 -----lllllllllll------
Δ = -4 m = 0 ------llllllllll------
m = -2
+ + + + - + -2 ≤ m ≤ 0
llllllllllllllllllll ---lllll-----
3. Determine o período das funções:
a) y = sen7x
R: p = 2π/k
p = 2π/7
b) y = 3sen2x
R: p = 2π/k
p = 2π/2
p = π
c) y = 5sen (x/4 + π/5)
R: p = 2π/k
p = 2π / 1/4
p = 2π . 4
p = 8π
Δ > 0 --------- m/a , c/a , m/a -------- As vírgulas são X1 e X2 respectivamente
Δ = 0 --------- m/a , m/a --------------- X1 = X2
Δ < 0 --------- m/a
m/a = mesmo valor que A ( positivo ou negativo)
c/a = contrário do valor de A (positivo ou negativo)
